魔方陣

　　行は　　　2+9+4=15　　7+5+3=15　　6+1+8=15
　　列は　　　2+7+6=15　　9+5+1=15　　4+3+8=15
　　対角線は　2+5+8=15　　4+5+6=15
となって、確かに和がすべて等しくなっています。
　同じようにして4次魔方陣、5次魔方陣、6次魔方陣・・・があります。下の例を見て行、列、対角線の和が等しくなっていることを確認してみてください。縦、横、対角線の数の和を定和といいます。ｎが決まれば定和も決まります。3次では15、4次では34、5次では65…となります。ｎ次魔方陣の定和は、1〜ｎ²の合計をｎで割れば出ますから、
　定和＝ｎ（ｎ²+1）／２
と計算されます。
　魔方陣は英語では magic square です。昔からヨーロッパでも中国でも、魔方陣は神秘的なものとして多くの人を魅了してきました。現在でも魔方陣の研究をしている人がたくさんいます。昔と違ってコンピュータという道具があるので、いろいろなことが分かってきましたが、コンピュータを以ってしても分からない謎もたくさん残されています。
　なお、｢悪魔くん｣や｢グルグル｣にでてくる｢魔法陣｣はまったく別の物です。

・魔方陣の解はいくつある
　さて、このような魔方陣を作るにはどうしたらいいでしょうか。3次魔方陣ならば少し考えるだけでも求められると思いますが、4次以上はなかなかできないでしょう。なにかひとつでもできればいいというのならWikipediaなどでも、いろいろな方法が紹介されています。でもひとつだけではつまらないでしょう。解（答え）をひとつ出すだけでなく、全部で何通りあるのかに興味がもたれます。
　解がいくつあるかを考えるときは、回転や裏返しをどうするか決めておかないと話が混乱してしまいます。たとえば、上の3次魔方陣で全体を90°右回転したものも魔方陣になっています（数字の向きは直してくださいね）。同様に180°、270°回転したパターンも魔方陣です。さらにそれらを裏返したものも魔方陣です。そうすると１つの解から７つの解が簡単に求められます。実際に解を数えるときは、このように回転や裏返しで一致するようなものは一種類として数えることにします。
　それで、n次魔方陣の解の個数は何か公式でもあって簡単に求められると思われるかもしれません。ところが公式などはなくて、とにかく全部計算してみないと分からないという厄介な問題なのです。今わかっている魔方陣の解の数は以下の通りです。

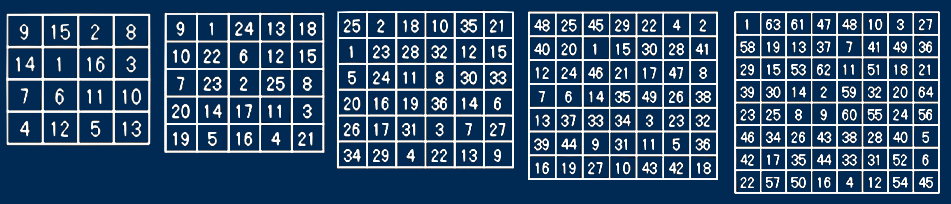
　　　　3次　　　　　　　1
　　　　4次　　　　　　880
　　　　5次　275,305,224
　　　　6次　　 約1800京



・３次魔方陣
　3次魔方陣の解は上に示した１つだけです。変数が9個で、和が一定という条件が8つ（実質7つ）もあるのに、1から9を全部使った解が存在するというのはある意味で奇跡かもしれません。左上から「憎し、七五三、無為や(294753618)」と語呂合わせで覚えるといいでしょう。

・４次魔方陣
　4次魔方陣は880種あります。これはコンピュータが発明される以前にすべて求められていました。現在ならパソコンですぐに全部の答えをだせるでしょう。プログラミングの演習問題として手ごろなところだと思います。
　　→ 4次魔方陣の性質 　　→ 特殊な4次魔方陣 　　→ 4次魔方陣のすべて 　　→ 4次魔方陣を求めるプログラム

・５次魔方陣
　5次魔方陣はなんと、275,305,224（約3億）もあります。これは1973年にアメリカのシュレーペルがコンピュータですべてを計算して初めてわかったことです^*1。しかし残念なことに、このことはあまり話題にされなかったので、その後20年以上たっても5次魔方陣の総数は不明と書いてある本がありました。この計算は1970年代のコンピュータにとっては大仕事でした。大変な計算時間がかかったそうです。今なら、多少待ち時間が長くなりますがパソコンで計算できます。ただし、プログラムを組むのはそんなに簡単ではないかも知れません。当研究室でも以前、卒業研究ですべて計算を行いました。
　　→ 特殊な５次魔方陣

・６次魔方陣
　5次魔方陣でこれだけの数になると６次魔方陣はいったいどれだけ多くなるのでしょうか。正確な数は現在わかっていません。それは最新のスーパーコンピュータを使ったとしてもとても計算しきれないからです。でも、およその数ならわかります。1992年に｢ランダムサンプリングによる推定｣という方法を使って、当研究室で計算されました^*2。その数は1.8×10¹⁹です。つまり
　　約 1800京
になります。後の1998年にドイツのK.PinnとC.Wieczerkowskiもほぼ同じ数（1.775×10¹⁹）を出しています。

・７次以上の魔方陣
　7次以上の魔方陣も相当たくさん存在すると予想されます。上に出てきたK.PinnとC.Wieczerkowskiは次の7次魔方陣についても計算し、3.760×10³⁴と見積もりました。この辺になると、素粒子論とか宇宙論でしか現れない数字ですね。
　その後、さらに次数があがり、W.Trumpは20次魔方陣が1.810×10⁷⁴⁴と計算しています。そして北島顕正さんは30次まで計算して6.56×10²⁰⁵⁶だと述べています。10の2000乗なんてどんな物理学でも出てこない数です。
　このように７次以上の魔方陣はあまりにも数が多く、計算も面倒なので、パズルとして楽しむには不向きです。単に魔方陣の性質だけでなく他の条件も合わせた特殊な魔方陣が話題になる程度です。

・完全魔方陣
　完全魔方陣とは、行、列、２つの対角線だけでなく、すべての汎対角線の和が等しくなる魔方陣です。汎対角線とは右の図のように斜めにたどっていき、左右の端に来たら反対側に続くラインです。これは魔方陣の右端と左端がつながっていると考えたときの斜め線と言えます。また、同様に上の行と下の行もつながっていると考えられます。
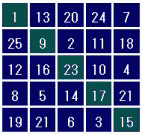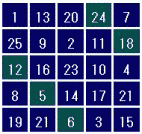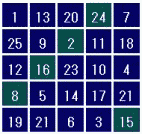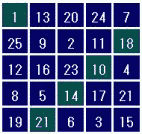　汎対角線上の和が等しいということは、行や列をローテーションしても魔方陣になっているということです。ですから、n次の完全魔方陣1個からn²個の魔方陣が作れます。
　完全魔方陣はただの魔方陣よりきつい条件なので、その数はずっと少なく、次数によっては１つも存在しません。次数ごとの完全魔法陣の数は 特殊な4次魔方陣、 特殊な５次魔方陣、 特殊な６次魔方陣の説明を参照してください。

・１〜ｎ²以外の数を使う魔方陣
　使う数を特別な数に限定した魔方陣があります。

* 素数魔方陣

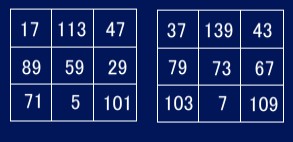
　最も有名なのは素数だけを使った魔方陣です。右に3次の素数魔方陣の例を示します。3次といえども、使える数が素数だけとなると探すのも大変です。小さい素数では魔方陣を作るのは難しく、100より小さい素数だけではできないようです。でも、素数は無限に存在しますから、3次の素数魔方陣も無限に存在すると思われます。なお、古い文献を見ると「１も素数とみなす」というのがよくありますが、これはフェアではないですね。1は素数ではありませんから。
→ 3次素数魔方陣

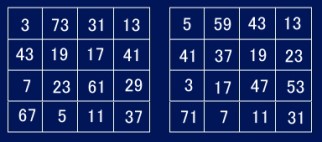　同様に4次の素数魔方陣も作ることができます。右は4次の素数魔方陣で、定和が最小（120）のものです。3次よりも定和を小さくできるというのは面白いですね。
　4次の素数魔方陣の中には完全魔方陣（汎対角線の和も一定）もあります。
→ 4次素数魔方陣


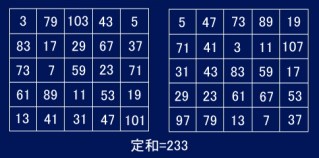　次は5次です。あてずっぽうに探しても大変ですから、定和がなるべく小さいものを探してみましょう。使う素数は2を含まないことは明白です。そこで3以上で小さい方から25個（3，5，…101）を使ってできるかというと、それは不可能です。なぜなら3〜101の合計は1159で5の倍数でないからです。1159÷5＝231.8ですから、定和で考えると少なくとも233以上になるはず。そこで定和233を探してみると、驚くことに次から次へと見つかりました（かるく10万を超えます）。その内の2つを右に示します。
→ 5次素数魔方陣

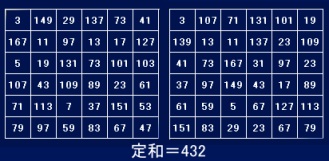　6次はどうでしょう。5次の場合と同様にして、なるべく小さい素数を使って和が6の倍数になる組み合わせを捜します。そうすると、可能性のある定和での最小は432になります。そこで定和を432の解があると仮定して調べると、これまたたくさん出てきました。
→ 6次素数魔方陣



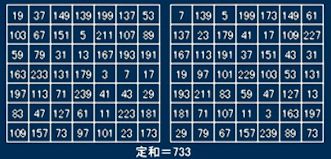　7次も同じように考えます。5次、6次と同様に3からの小さい方の49個の素数では和が7の倍数にはなりません。それで、和が7の倍数で最小になるような組み合わせを探しました。和が5131になる組み合わせが2通りあって、そのときの定和は733です。
　この定和733の解があるかどうか分かりませんが、5次、6次からの流れから予想するとたくさん解がありそうです。ただ、7次ともなると並べ方を小さい順に調べていくと、最初の解が出てくるのに相当時間がかかりそうです。もちろん全解検索も無理です。
　そこで、いくつかのセルに適当に数を置いて、残りを計算するという方法をとりました。その結果、やはり多くの7次素数魔方陣を見つけることができました。右に2つの例を示します。
→ 7次素数魔方陣
　8次，9次も同様にして求めました。8次の最小定和は1154，9次の最小定和は1731です。
→ 8次素数魔方陣　　 → 9次素数魔方陣

　その他の素数魔方陣
　素数魔方陣の資料を探していると，最小定和よりも「連続する素数」にこだわる人が多いことが分かります。途中が抜けることがないような素数列で魔方陣を構成するのです。したがって定和は素数魔方陣の最小定和より大きくなります。4〜9次の連続素数魔方陣は40年以上前から，阿部楽方氏や鈴木昭雄氏が作られたものが知られています。しかし，3次についてはもう少し後になって見つかりました（H. L. Nelson, Journal of Recreational Mathematics, 1988, vol. 20:3, p.214 ）。というのもとてつもなく大きい数でしか見つけられないからです。 → 3次連続素数魔方陣
　次数の大きい方はこのページにたくさん例が出ています。
http://digilander.libero.it/ice00/magic/prime/orderConstant.html

　次は平方数（整数を2乗した数）だけの魔方陣です。平方数は、1、4、9、16、25、… というように、徐々に間隔が広がっていくので定和がどうしても大きくなります。古くは1770年にオイラーが手紙の中で4次の平方数魔方陣を書いていたと言われています。その平方数魔方陣の定和は8515でした。最小定和についての記述は、パズル懇話会で小林壽雄さんが発表された4次平方数魔方陣（定和＝2823）を見たのが最初でした。
　調べて見ると平方数魔方陣は、4次、5次，…とたくさん存在します。ところが3次はひとつも見つかりません。たぶん存在しないと思われますが、存在しないという証明を見たこともありません。

　4次では平方数魔方陣がたくさん見つかります。それでも定和の最小は2823とかなり大きい数でした。5次も同様ですが、最小定和は4次より小さくて1375でした。
　6次も1から36の平方数を使って魔方陣が作れないことは計算で確認しました。ネットで検索したら定和が2551のものが出ていましたが，残念ながら 0 を使うという変則的な平方数魔方陣でした。計算して定和2779を見つけたのですが，小林壽雄さんからもっと小さい定和2775があることを教えていただきました。なんと1994年に既に計算されていたそうです。 → 0を許せば

→ 4次平方数魔方陣　　→ 5次平方数魔方陣　　→ 6次平方数魔方陣

・魔方陣の神秘性？ （おまけ）

　魔方陣は純粋に数学的問題ですが、昔の人は「どこでも和が一定」という性質は不思議に感じられたことでしょう。魔方陣は魔法陣のように占いなどに使われていたようです。魔方陣が神秘的だという例としてよく取り上げられるのが、デューラーのメランコリアです。デューラー（1471-1528）はルネッサンス期の画家でメランコリアはその代表作です。右の図ではよくわかりませんが赤枠で示した部分が4次魔方陣になっています。下はそれを写したものです。
　この魔方陣の何が不思議なのでしょう。それは最下行の中央の２つの数が1514と並んでいて、この絵の描かれた年を表しているというのです。さあ、これは偶然なのか故意なのかどっちでしょう。もし、わざと1514が入るように魔方陣を作ったとしたら相当大変な計算をしたのでしょうか。
　この魔方陣，よく見ると数の並びが非常に規則的で、よくある初歩的な魔方陣の作り方の例にもなっているものです。そう考えると1514が制作の年と一致しているというのは後で見つけた偶然の一致でしょう。

* 4次魔方陣と誕生日
　では年ではなくて月日はどうでしょう。4次魔方陣に自分の誕生日が入っていたら面白いと思いませんか。
　そこで、どんな日付なら魔方陣の中に入れられるか考えてみましょう。すぐに分かるのは17以上の日は無理だということ。そしてゾロ目の日の人も残念です。では、その他はどんな日でもできるのでしょうか。
　4次魔方陣でどこでもいいから横に連続する2マスを月日とすると。上で無理だといった日以外はほとんどが可能です。ここで、また残念な誕生日は
　　7月8日　　8月7日　　9月10日　　10月9日
の4日だけです。結局1年365日のうち176日が可能です。およそ半数の人は4次魔方陣の中に自分の誕生日を見つけることができるというわけですね。そう考えるとあんまり神秘的でもないか？

* 6次魔方陣と誕生日
　4次魔方陣では16より大きい数は出てきません。全ての月日を魔方陣に入れようとすると31までの数が必要なので、最小でも6次魔方陣になります。では逆に、6次魔方陣ならどんな月日でも入れることは可能でしょうか。答えはYES。2月29日も含めて横並びの2マスに月日を並べることができます。
　どうやって証明したか…。まったくエレガントではありません。366日すべて(ゾロ目の日を除く)について、少なくとも1個の魔方陣が存在する実例を求めました。せっかく計算したので結果を載せておきます．
　→ 月日を含む6次素数魔方陣（1-6月） 　　→ 月日を含む6次素数魔方陣（7-12月）

・魔方陣パズル
　未完成の魔方陣を完成させる問題です。4次魔方陣の条件に合うように1〜16を重複なく入れてください。難易度は4段階に分かれています。効率よく解くには、行、列、対角線の和だけでなく、四隅や中央の４数などの和も利用します（→ 4次魔方陣の性質）。
　このような魔方陣の問題は、いい加減につくると答えがいくつも出てきてしまいます。それでは面白くないので、ここでは数独（→ ペンシルパズル）のように、答えは1つしかないということにします。

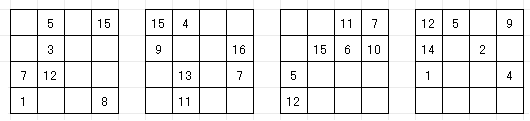
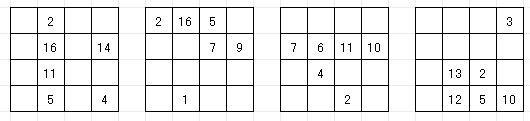
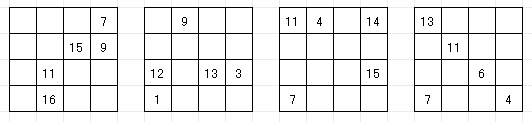
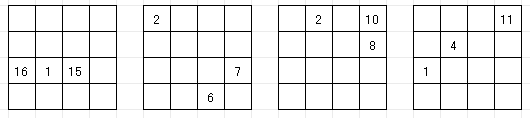
解答
→ EASY　 → MEDIUM　 → HARD 　 → VERY HARD

・魔方陣パズルの最少ヒント数
　数独において解が１つに定まる問題のヒントの数の最少はいくつか？という問題がありました。ヒント17個の問題がいくつか知られていましたが、ヒント16個以下でそのような問題はない、と証明されたのは2012年のことでした^*3。魔方陣の問題でも同じことが考えられます。ヒントが少なければ答がいっぱい出てきます。ちょうど1個だけに定まるようなヒントの個数の最少はいくつでしょう。

* 3次魔方陣の問題
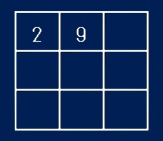　3次魔方陣では、最少ヒント数は2個です。1個では回転や裏返しが禁止できませんからどうしても２個必要になります。右図は2個の例ですが、4隅のどれかと辺の真ん中のどれかの数をヒントとすれば解は一意に決まります。



* 4次魔方陣の問題
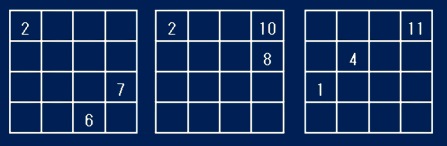
　4次魔方陣では、2個だけで解が一意に決まるようなヒントの組み合わせはありません。どうしても3個は必要になります。ここに示したもの以外にもいくつかあります。上のVERY HARDの問題がこれです。



* 5次魔方陣の問題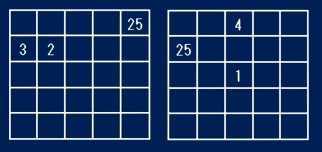
　5次の場合も2個で一意の解になるヒントはありませんでした。すべての2つのセルの配置にすべての数の組み合わせを置いてみても解が1つになることはありませんでした。
　最少のヒント数は3です。ここに示した2つはその例ですが、基本的にこの2つのパターンだけしかありません。パターンというのは、これらの回転、裏返し、26の補数どうしの入れ替え、2-4行、2-4列の入れ替えなどで簡単に変換できるものは1つと数える場合の数え方です。これも全部の場合を計算しましたが、かなり待ちくたびれる計算でした。

・その他の話題

* ヘテロ方陣 （天邪鬼な方陣）
　右の方陣を見てください。魔方陣ではありませんね。ではどんな特徴があるのでしょうか。実はすべての行，列，対角線の和の値が異なっているのです。魔方陣とは全く反対の方陣です。正式な呼び名かどうか分かりませんがヘテロ方陣と呼ぶようです。　それで，ヘテロ方陣というのはそんなに珍しいのでしょうか。
　3×3の方陣は回転裏返しを同一視すると45360（9!/8）通りあります。そのうちで魔方陣はたったの１つ。ヘテロ方陣はというと，3120通りあります。ですから，そんなに珍しいものではありません。でも，手計算で作ろうとすると，なかなか面倒な作業です。
　では，もう一歩進んで，すべての行，列，およびすべての汎対角線の和が異なる方陣，いわば完全ヘテロ方陣というのはできるでしょうか…。残念ながら3次では不可能です。4次以上なら右の図のようにできます。

* 魔方陣でスライドパズル
　整列状態の3次方陣の中央の5を抜きます。そしてスライドして再び5を入れると魔方陣になります。簡単そうですが，最低でも16手もかかります。

* クロスワードっぽい魔方陣の問題
　数字は与えられていません。ヒントを頼りに魔方陣を完成させてください。 → 問題


* 魔方陣 ID
　何が魔方陣なんでしょう。
→ ID1　 → ID2　 → ID3　 → ID4　 → ID5　 → ID6　

参考文献： 方陣の研究 大阪教育図書 1983年 平山, 阿部　（魔方陣全般を非常に詳しく解説しています）
　　　　 　　^*1Scientific American 1/1976 (Martin Gardnerによる紹介）
　　　　 　　^*2｢ランダムサンプリングによる6次魔方陣の総数の推定｣数芸パズル第177号 1992年4月 pp13-20 大石　 　　 → PDF
　　　　 　　^*3ペンシルパズル