特殊な６次魔方陣

・内包魔方陣
　内包魔方陣とは、全体が魔方陣であって、さらに内部に縦横対角線の和が等しい正方形の領域を持つものです。次数が増えて６次ともなると、いろいろな内包魔方陣ができます。いろいろなパターンがありますが、単純で美しいものから紹介します。

６-４魔方陣
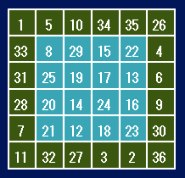　６次魔方陣の中央に４次の方陣が入っているものです。この解は7,736,347,893,760通り（約8兆）あります。そんなに沢山を数えるのはさぞかし大変だと思うかもしれませんが、計算は意外と単純です。
　まず条件をよく調べると内側の４方陣の定和は74に決まってしまいます。また、内側の４方陣と外枠（図の緑の部分）はお互いに干渉しないので、それぞれの個数を計算して掛ければいいのです。さらに４方陣は回転、裏返しが可能ですし、外枠は2〜4行、2〜4列を任意の順に入れ替えることができます。それらを考えると計算量は相当減らすことができます。
［この数は91年度の卒研で大橋聖君と若林道生君が確認してくれました．］


６-４-４魔方陣
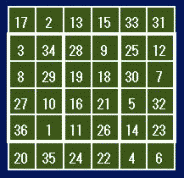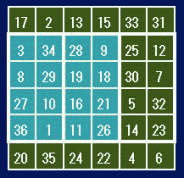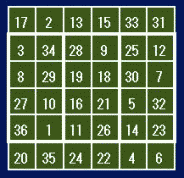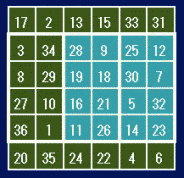　６次魔方陣の中に４方陣がふたつ入っているものです。この解は1,010,688通りあります。６次の中に４次がふたつのパターンはこの形だけです。





６-４-３魔方陣
　６次魔方陣の中に４方陣と３方陣が入っているもので、下の図のような３つのパターンがあります。
　　�T型は1120通り
　　�U型は12通り
　　�V型は608通り
見つかりました。